Vue diff算法

先阅读尤大的文章：

https://www.zhihu.com/question/31809713/answer/53544875

比较innerHTML和Virtual DOM的重绘性能消耗

innerHTML:render html string O(template size)+重新创建所有DOM元素O(DOM size)

Vitual DOM :render Vitual DOM +diff O(template size)+必要的DOM更新O

Vitual DOM render+diff显然比渲染html字符慢，但是它依然his纯js层面计算，比DOM操作而言，便宜了很多

diff算法：

一、是什么

diff算法是一种同层的树节点进行比较的高效算法

两个特点：

比较只会在同层级进行，不会跨层级比较

在diff比较过程中，循环会从两边向中间比较

diff 算法的在很多场景下都有应用，在 vue 中，作用于虚拟 dom 渲染成真实 dom 的新旧 VNode 节点比较

二、比较方式

diff整体策略为：深度优先，同层比较

1. 比较只会在同层级进行, 不会跨层级比较

1. 比较的过程中，循环从两边向中间收拢

下面举个vue通过diff算法更新的例子：

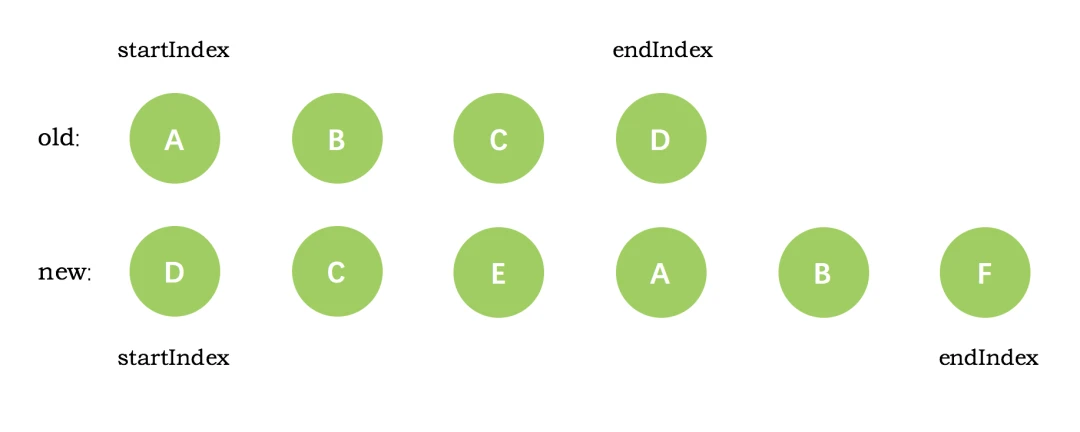
新旧VNode节点如下图所示：

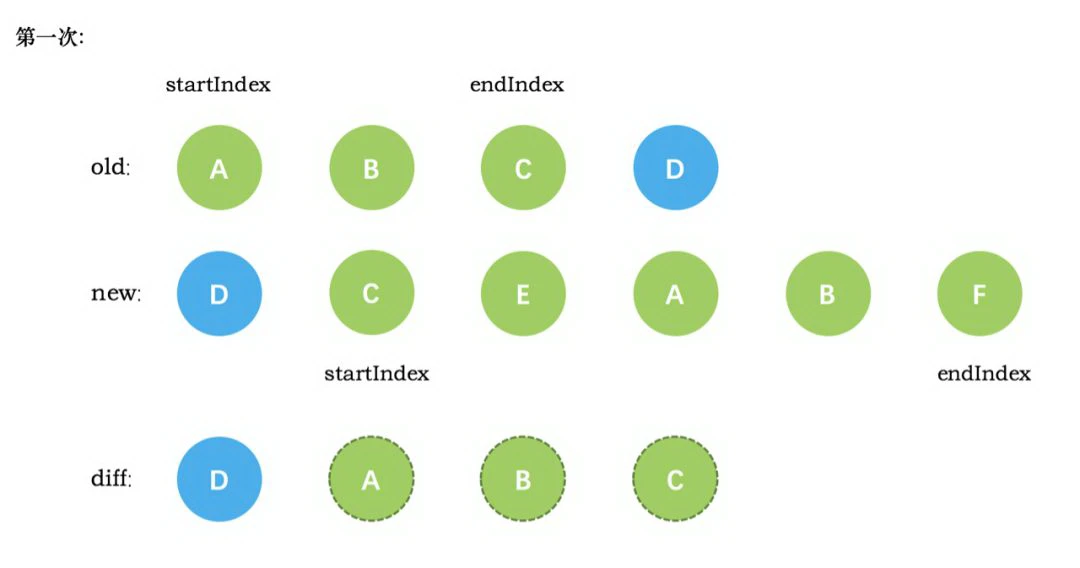
第一次循环后，发现旧节点D与新节点D相同，直接复用旧节点D作为diff后的第一个真实节点，同时旧节点endIndex移动到C，新节点的 startIndex 移动到了 C

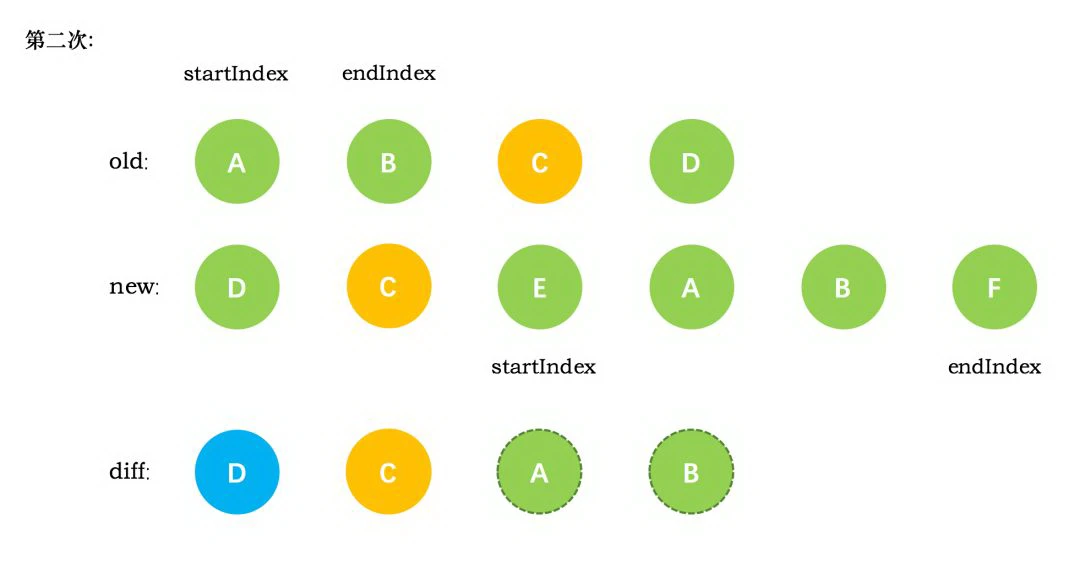
第二次循环后，同样是旧节点的末尾和新节点的开头(都是 C)相同，同理，diff 后创建了 C 的真实节点插入到第一次创建的 B 节点后面。同时旧节点的 endIndex 移动到了 B，新节点的 startIndex 移动到了 E

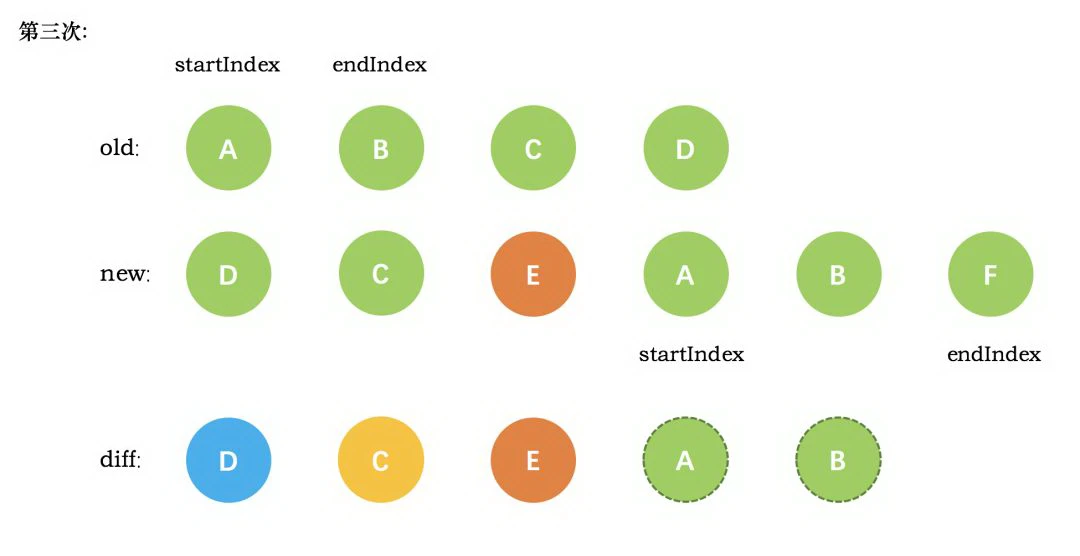
第三次循环中，发现E没有找到，这时候只能直接创建新的真实节点 E，插入到第二次创建的 C 节点之后。同时新节点的 startIndex 移动到了 A。旧节点的 startIndex 和 endIndex 都保持不动

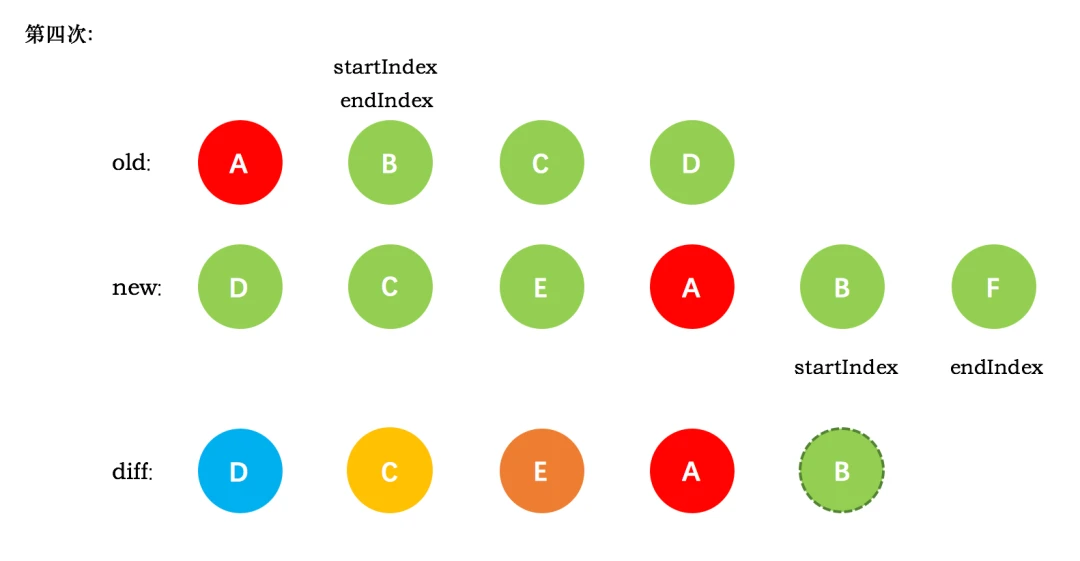
第四次循环中，发现了新旧节点的开头(都是 A)相同，于是 diff 后创建了 A 的真实节点，插入到前一次创建的 E 节点后面。同时旧节点的 startIndex 移动到了 B，新节点的 startIndex 移动到了 B

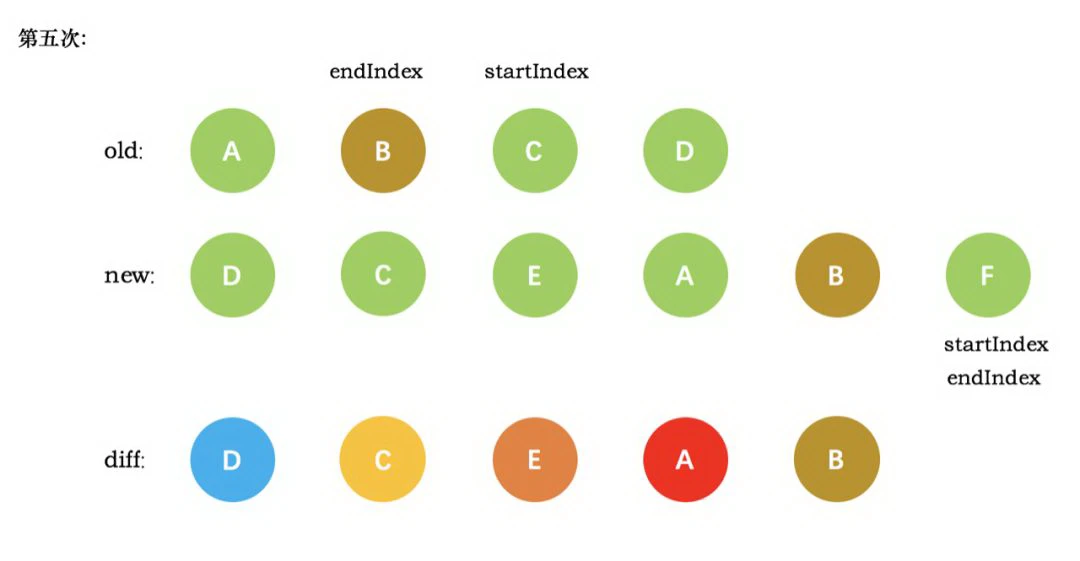
第五次循环中，情形同第四次循环一样，因此 diff 后创建了 B 真实节点 插入到前一次创建的 A 节点后面。同时旧节点的 startIndex 移动到了 C，新节点的 startIndex 移动到了 F

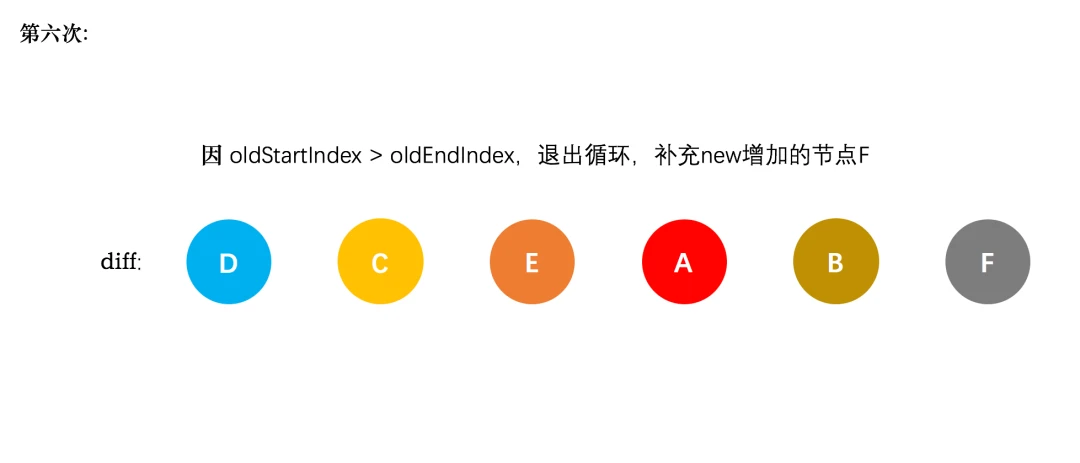
新节点的 startIndex 已经大于 endIndex 了，需要创建 newStartIdx 和 newEndIdx 之间的所有节点，也就是节点F，直接创建 F 节点对应的真实节点放到 B 节点后面

三、原理分析

当数据发生改变时，set方法会调用Dep.notify通知所有订阅者Watcher，订阅者就会调用patch给真实的DOM打补丁，更新相应的视图

Vue2中使用双端diff算法：

//双端diff算法
function patchKeyedChildren(n1,n2,container) {
    const oldChildren = n1.children
    const newChildren = n2.children
    //是个索引值
    let oldStartIdx = 0
    let oldEndIdx = oldChildren.length-1
    let newStartIdx = 0
    let newEndIdx = newChildren.length-1
    //四个索引指向的vnode
    let oldStartVnode = oldChildren[oldStartIdx]
    let oldEndVnode = oldChildren[oldEndIdx]
    let newStartVnode = newChildren[newStartIdx]
    let newEndVnode = newChildren[newEndIdx]
     //如果头尾部找不到复用的节点，只能拿新的一组子节点中的头部节点去旧的一组子节点中寻找
     while(oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
        //如果旧结点数组中头部结点或者尾部结点为undefined，说明已经被处理过了，直接跳到下一个位置
        if(!oldStartVnode) {
            oldStartVnode = oldChildren[++oldStartIdx]
        }else if(!oldEndVnode){
            oldEndVnode = oldChildren[--oldEndIdx]
        }
        else if(oldStartVnode.key === newStartVnode.key){
            patch(oldStartVnode,newStartVnode,container)
            //更新相关索引
            oldStartVnode = oldChildren[++oldStartIdx]
            newStartVnode = newChildren[++newStartIdx]
        }//结点在新的顺序中仍处于尾部，不需要移动，打补丁后更新索引和头尾部结点变量
         else if(oldEndVnode.key === newEndVnode.key){
            patch(oldEndVnode,newEndVnode,container)
            oldEndVnode = oldChildren[--oldEndIdx]
            newEndVnode = newChildren[--newEndIdx]
        }else if(oldStartVnode.key === newEndVnode.key){
            patch(oldStartVnode,newEndVnode,container)
  //原本是头部结点，在新的顺序中变为了尾部结点，将旧结点对应的真实DOM移动到旧的一组子节点的尾部结点所对应的真实DOM后面，更新索引         				  
            insert(oldStartVnode.el,container,oldEndVnode.el.nextSibling)
            oldStartVnode = oldChildren[++oldStartIdx]
            newEndVnode = newChildren[--newEndIdx]
    
        }else if(oldEndVnode.key === newStartVnode.key){
            patch(oldEndVnode,newStartVnode,container)
            //结点p-4原本是最后一个子节点，在新的顺序中它变成了第一个子节点，因此，将索引oldEndIdx指向的虚拟结点对应的真实DOM移动到索引oldStartIdx指向得到虚拟结点所对应的真实DOM前面
            insert(oldEndVnode.el,container,oldStartVnode.el)
            oldEndVnode = oldChildren[--oldEndIdx]
            newStartVnode = newChildren[++newStartIdx]
        }else {
            //遍历旧的一组子节点，试图寻找与newStartVnode拥有相同key的节点
            //idxInOld就是新的一组子节点的头部节点在旧的一组子节点中的索引
            const idxInOld = oldChildren.findIndex(
                node=>node.key===newStartVnode.key
            )
            //idxInOld大于0说明·找到了可以复用的结点，并且需要将其对应的真实DOM移动到头部
            if(idxInOld > 0){
                //idxInOld位置对应的vnode就是需要移动的结点
                const vnodeToMove = oldChildren[idxInOld]
                patch(vnodeToMove,newStartVnode,container)
                //将vnodeToMove移动到头部结点oldStartVnode.el之前
                insert(vnodeToMove.el,container,oldStartVnode.el)
                //由于位置idxInOld处的结点所对应的真实DOM已经移动到了别处，因此将其设置为undefined
                oldChildren[idxInOld] = undefined


            }else{
                //将newStartVnode作为新节点挂载到头部，使用当前头部结点oldStartVnode.el作为锚点
                patch(null,newStartVnode,container,oldStartVnode.el)
            }
            //更新newStartIdx
            newStartVnode = newChildren[++newStartIdx]
        }       
    }
    //如果oldStartIdx已经大于oldEndIdx，但是newStartIdx<=newEndIdx,说明新节点中还有元素未被挂载,需要挂载它们
    if(oldEndIdx < oldStartIdx && newStartIdx <= newEndIdx){
        for(let i = newStartIdx; i<=newEndIdx ; i++){
            patch(null,newChildren[i],container,oldStartVnode.el)
        }
    }
    //如果newStartIdx已经大于newEndIdx,而oldStartIdx小于等于newEndIdx,则旧的结点中有结点需要移除
    if(newEndIdx < newStartIdx && oldStartIdx<=oldEndIdx) {
        for(let i=oldStartIdx;i<oldEndIdx;i++){
            unmount(oldChildren[i])
        }
    }

}
function insert(el,parent,anchor=null){
    parent.insertBefore(el,anchor)
}

Vue3快速diff算法

在实测中性能最优，它借鉴了文本Diff中的预处理思路，先处理新旧两组结点中相同的前置结点和相同的后置结点，当前前置结点和后置结点全部处理完毕后，如果无法简单地通过挂载新节点或者卸载已经不存在的结点来完成更新，则需要根据结点的索引关系，构造一个最长递增子序列，source数组，用来存储新的一组子节点在旧子节点中的位置索引,后面用它来计算最长递增子序列，最长递增子序列所指向的结点即为不需要移动的结点

function patchKeyedChildren(n1,n2,container) {
    //更新相同的前置结点
    let j = 0;
    let oldVnode = oldChildren[j]
    let newVnode = newChildren[j]
    while(oldVnode.key === newVnode.key) {
        patch(oldVnode,newVnode,container)
        j++
        oldVnode = oldChildren[j]
        newVnode = newChildren[j]
    }
    //更细相同的后置结点
    //索引oldEnd指向旧的一组子节点的最后一个结点
    let oldEnd = oldChildren.length-1
    let newEnd = newChildren.length-1
    oldVnode = oldChildren[oldEnd]
    newVnode = newChildren[newEnd]
    //while循环从后向前遍历，直到遇到拥有不同key值的结点为止
    while(oldVnode.key === newVnode.key){
        patch(oldVnode,newVnode,container)
        oldEnd--;
        newEnd--;
        oldVnode=oldChildren[oldEnd]
        newVnode=newChildren[newEnd]
    }
    //预处理完毕，如果j>oldEnd并且j<=newEnd,说明从j到newEnd之间的结点应该作为新节点插入
    if(j>oldEnd && j<=newEnd) {
        //锚点索引
        const anchorIndex = newEnd+1
        //锚点元素
        const anchor = anchorIndex < newChildren.length ? newChildren[anchorIndex].el :null
        //挂载新节点
        while(j<newEnd){
            patch(null,newChildren[j++],container,anchor)
        }
    }else if(j>newEnd&&j<=oldEnd){
        //j到oldEnd之间的结点应该被卸载
        while(j<=oldEnd){
            unmount(oldChildren[j++])
        }
    }else{
        //构造source数组，用来存储新的一组子节点在旧子节点中的位置索引,后面用它来计算最长递增子序列
        const count = newEnd -j+1
        const source =newArray(count)
        source.fill(-1)
        //新增pos和move用来判断结点是否需要移动
        let move =false
        let pos =0
        //oldStart和newStart分别为起始索引，即j
        const oldStart = j
        const newStart = j
        //构建索引表,存储新子节点数组中键值和索引
        const keyIndex = {}
        for(let i = newStart;i<=newEnd;i++){
            keyIndex[newChildren[i].key]=i
        }
        //新增patched代表更新过的结点数量
        let patched = 0;
        //遍历旧的一组子节点
        
        for(let i = oldStart;i<=oldEnd;i++){
            const oldVnode = oldChildren[i]
          //更新过的结点数量小于等于需要更新的结点数量，执行更新
            if(patched<=count){
                //通过索引表快速找到新子节点中和旧子节点有相同key的结点位置
                const k= keyIndex[oldVnode.key]
                if(typeof key !== "undefined"){
                    newVnode = newChildren[k]
                    //调用patch函数完成更新
                    patch(oldVnode,newVnode,container)
                    patched++;
                    //填充source数组
                    source[k-newStart]=i
                    if(k<pos){
                        move=true
                    }else{
                        pos=k;
                    }
                }else{
                    unmount(oldVnode)
                }

            }else{//更新过的结点数量大于需要更新的结点数量，则卸载多于的结点
                unmount(oldVnode)

            }
        }
        if(move){
            //如果move为真，则需要进行DOM移动操作
            const seq = lis(sources)//[0,1]计算最长递增子序列的索引信息
            //s指向最长递增子序列的最后一个元素
            let s=seq.length-1
            let i=count-1
            for(i;i>=0;i--){
                if(source[i]===-1){
                    //说明索引为i的结点为全新的结点，挂载
                    //该结点在新子节点中的索引
                    const pos=i+newStart
                    const newVnode = newChildren[pos]
                    //该结点的下一个结点的位置索引
                    const newPos=pos+1
                    //锚点
                    const anchor = newPos <newChildren.length?newChildren[newPos].el:null
                    //挂载
                    patch(null,newVnode,container,anchor)
                }else if(i!==seq[s]){//说明节点需要移动
                    //该结点在新子节点中的索引
                    const pos=i+newStart
                    const newVnode = newChildren[pos]
                    //该结点的下一个结点的位置索引
                    const newPos=pos+1
                    //锚点
                    const anchor = newPos <newChildren.length?newChildren[newPos].el:null
                    //移动
                    insert(newVnode.el,container,anchor)
                }else{
                    //当i===seq[j],说明该位置结点不需要移动,让s指向下一个位置
                    s--
                }
            }
            
        }

    }

}
function lis(arr) {
    let len = arr.length,
      res = [],
      dp = new Array(len).fill(1);
    // 存默认index
    for (let i = 0; i < len; i++) {
      res.push([i])
    }
    for (let i = len - 1; i >= 0; i--) {
      let cur = arr[i],
        nextIndex = undefined;
      // 如果为-1 直接跳过，因为-1代表的是新节点，不需要进行排序
      if (cur === -1) continue
      for (let j = i + 1; j < len; j++) {
        let next = arr[j]
        // 满足递增条件
        if (cur < next) {
          let max = dp[j] + 1
          // 当前长度是否比原本的长度要大
          if (max > dp[i]) {
            dp[i] = max
            nextIndex = j
          }
        }
      }
      // 记录满足条件的值，对应在数组中的index
      if (nextIndex !== undefined) res[i].push(...res[nextIndex])
    }
    let index = dp.reduce((prev, cur, i, arr) => cur > arr[prev] ? i : prev, dp.length - 1)
    // 返回最长的递增子序列的index
    return result[index]
  }
  

时间复杂度：

1.传统diff算法中，通过循环递归对结点进行比较，同层级比较的时候就算使用动态规划（参考编辑距离），时间复杂度最坏为O(n^2),树递归比较的话，复杂度为O(n^3)

2.React的开发者结合Web界面的特点做出了两个大胆的假设，使得Diff算法复杂度直接从O(n^3)降低到O(n)，假设如下：

两个相同组件产生类似的DOM结构，不同的组件产生不同的DOM结构；
对于同一层次的一组子节点，它们可以通过唯一的id进行区分。
通过这两个假设，他们提供了下面的Diff算法思路，diff算法过程中使用优先判断和就地复用策略提高效率

(1).同层比较

新的Diff算法是逐层进行比较，只比较同一层次的节点，大大降低了复杂度

(2).不同类型结点的比较

如果新旧结点类型不同，diff算法会字节删除旧的结点及其子节点并插入新的结点，这是由于前面提出的不同组件产生的DOM结构一般是不同的，所以可以不用浪费时间去比较。注意的是，删除节点意味着彻底销毁该节点，并不会将该节点去与后面的节点相比较。

（3）相同类型结点比较

diff算法更新结点的属性实现转换

（4）列表结点需要给key进行高效比较